What is Differentiation? It is an organized yet flexible way of proactively adjusting teaching and learning to meet kids where they are and help them to achieve maximum growth as learners. (Tomlinson, 1999)
Differentiation in Math Should:
- Focus of instruction must be on key mathematical concepts (big ideas)
- Ensure prior assessment in order to determine what specific needs students have (cognitive development, mathematical sophistication)
- Provide student choice in terms of the details of the learning task, how the task can be done and how it is assessed.
- Understand learning needs through assessment in order to select learning strategies
Why Differentiate? To Meet Students Needs!
- Providing tasks within a student’s zone of proximal development and ensuring each student has the opportunity to contribute to the class community is key to meeting students’ needs in math.
- Zone of Proximal Development: distance between the actual development level determined by independent problem solving and the level of potential development determined through problem solving under adult guidance or collaboration with peers.
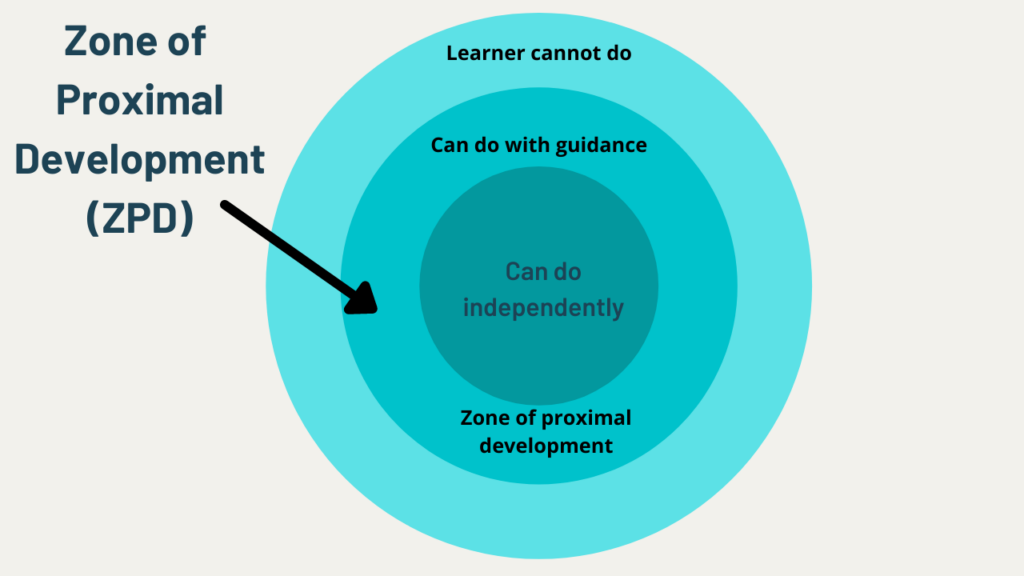
- By ensuring mathematical instruction falls into a student’s zone of proximal development a student is able to access new ideas that are beyond what they currently know but within their reach.
EXAMPLE LESSON:
- Lesson on calculating the whole, when a percent that is greater than 100% of the whole is known, using a problem such as: what number is 210% of?
- The skill the teacher might emphasize is solving proportions such as
but the more fundamental objective is getting students to realize that solving a percent problem is always about determining a ratio equivalent to one where the second term is 100.
- Differentiating the above problem, so that it falls within each student’s zone of proximal development might look like this:
- A teacher leads a lesson on what a percent is all about- even to students who do not have those abilities.
- The teacher allows less developed students to explore the idea of determining equivalent ratios to solve problems using percents less than 100% with ratio tables or other strategies.
- The teacher allows more advanced students to use percents greater than 100% and more formal strategies.
- **Only when the teacher feels that the use of percents greater than 100% and algebraic techniques where in an individual student’s zone of proximal development would they ask the student to work with those sorts of values and strategies.
- The skill the teacher might emphasize is solving proportions such as
References:
More Good Questions: Great Ways to Differentiate Secondary Mathematics Instruction, by Marian Small and Amy Lin, Hawker Brownlow Education, 2011, pp. 1–10.
“Differentiating Mathematics Instruction.” The Literacy and Numeracy Secretariat Government of Ontario,Capacity Building Series, Government of Ontario, Sept. 2008, www.edu.gov.on.ca/eng/literacynumeracy/inspire/research/capacityBuilding.html.